Jurnalis : Aisha Khalisa
Volume bangun ruang adalah salah satu konsep matematika yang sangat penting dalam memahami sifat-sifat benda tiga dimensi. Dalam kehidupan sehari-hari, kita sering berhadapan dengan objek-objek yang memiliki volume, seperti kotak, botol, atau bahkan bangunan. Memahami bagaimana menghitung volume tidak hanya berguna untuk ujian sekolah, tetapi juga untuk berbagai aplikasi praktis dalam bidang teknik, arsitektur, dan ilmu pengetahuan lainnya. Dengan mengetahui rumus dan cara menghitung volume, siswa dapat lebih mudah menyelesaikan soal-soal matematika yang berkaitan dengan bangun ruang. Artikel ini akan membahas secara lengkap berbagai jenis bangun ruang beserta rumus dan contoh soal yang bisa digunakan untuk meningkatkan pemahaman.
Bangun ruang terdiri dari berbagai bentuk, seperti kubus, balok, prisma, limas, tabung, kerucut, dan bola. Setiap bangun ruang memiliki rumus volume yang berbeda-beda, tergantung pada bentuk dan struktur geometrinya. Misalnya, volume kubus dihitung dengan mengalikan panjang sisi tiga kali, sedangkan volume tabung menggunakan luas alas dikali tinggi. Pemahaman dasar tentang masing-masing bangun ruang sangat penting agar tidak terjadi kesalahan dalam perhitungan. Selain itu, contoh soal yang diberikan dalam artikel ini akan membantu pembaca untuk melatih kemampuan mereka dalam menerapkan rumus-rumus tersebut.
Dalam dunia pendidikan, topik volume bangun ruang sering muncul dalam ujian nasional maupun ujian sekolah. Oleh karena itu, penting bagi siswa untuk memahami konsep ini secara mendalam. Artikel ini dirancang untuk memberikan informasi yang jelas dan terstruktur, sehingga pembaca dapat dengan mudah mengikuti langkah-langkah perhitungan dan memahami setiap tahapannya. Dengan demikian, artikel ini menjadi sumber referensi yang ideal bagi pelajar, guru, maupun orang tua yang ingin membantu anaknya belajar matematika dengan lebih efektif.
Jenis-Jenis Bangun Ruang dan Rumus Volume
Bangun ruang dibagi menjadi beberapa jenis berdasarkan bentuk permukaannya. Masing-masing jenis memiliki rumus volume yang berbeda. Berikut ini adalah penjelasan singkat mengenai beberapa bangun ruang utama beserta rumus volumenya.
-
Kubus
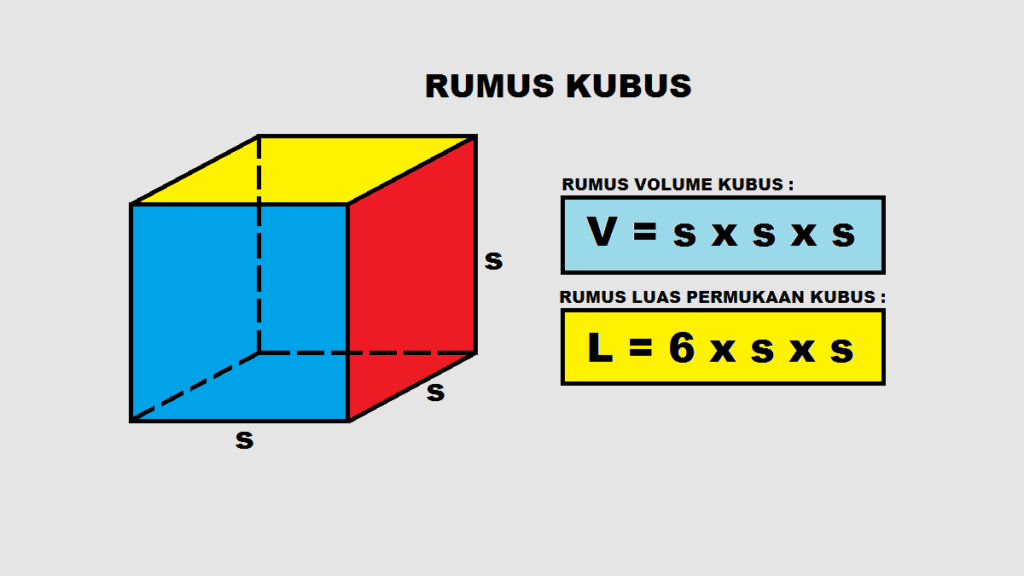
Kubus merupakan bangun ruang yang memiliki enam sisi persegi sama besar. Semua rusuk kubus memiliki panjang yang sama. Untuk menghitung volume kubus, rumus yang digunakan adalah:
$$
V = s^3
$$
di mana $s$ adalah panjang sisi kubus. -
Balok
Balok memiliki bentuk yang mirip dengan kubus, tetapi memiliki tiga pasang sisi yang berbeda. Balok memiliki panjang, lebar, dan tinggi yang berbeda. Rumus volume balok adalah:
$$
V = p \times l \times t
$$
di mana $p$ adalah panjang, $l$ adalah lebar, dan $t$ adalah tinggi balok. -
Prisma
Prisma adalah bangun ruang yang memiliki dua sisi identik di bagian atas dan bawah serta sisi tegak yang menghubungkannya. Volume prisma dapat dihitung dengan mengalikan luas alas dengan tinggi prisma:
$$
V = L_{\text{alas}} \times t
$$
Luas alas tergantung pada bentuk alas prisma, misalnya segitiga, persegi, atau lingkaran. -
Limas
Limas memiliki alas berbentuk segi banyak dan sisi-sisi tegak yang bertemu pada satu titik puncak. Rumus volume limas adalah:
$$
V = \frac{1}{3} \times L_{\text{alas}} \times t
$$
di mana $L_{\text{alas}}$ adalah luas alas dan $t$ adalah tinggi limas. -
Tabung
Tabung memiliki dua lingkaran sebagai alas dan sisi lengkung di antaranya. Volume tabung dihitung dengan rumus:
$$
V = \pi r^2 \times t
$$
di mana $r$ adalah jari-jari lingkaran alas dan $t$ adalah tinggi tabung. -
Kerucut
Kerucut memiliki alas berbentuk lingkaran dan satu titik puncak. Rumus volume kerucut adalah:
$$
V = \frac{1}{3} \times \pi r^2 \times t
$$
di mana $r$ adalah jari-jari lingkaran alas dan $t$ adalah tinggi kerucut. -
Bola
Bola adalah bangun ruang yang semua titik permukaannya memiliki jarak yang sama dari pusatnya. Rumus volume bola adalah:
$$
V = \frac{4}{3} \times \pi r^3
$$
di mana $r$ adalah jari-jari bola.
Contoh Soal dan Penyelesaian
Untuk memperdalam pemahaman tentang volume bangun ruang, berikut ini beberapa contoh soal beserta penyelesaiannya.
Contoh 1: Volume Kubus
Sebuah kubus memiliki panjang sisi 5 cm. Hitunglah volumenya!
Penyelesaian:
$$
V = s^3 = 5^3 = 125 \, \text{cm}^3
$$
Contoh 2: Volume Balok
Sebuah balok memiliki panjang 10 cm, lebar 6 cm, dan tinggi 4 cm. Hitunglah volumenya!
Penyelesaian:
$$
V = p \times l \times t = 10 \times 6 \times 4 = 240 \, \text{cm}^3
$$
Contoh 3: Volume Prisma Segitiga
Sebuah prisma segitiga memiliki luas alas 12 cm² dan tinggi prisma 8 cm. Hitunglah volumenya!
Penyelesaian:
$$
V = L_{\text{alas}} \times t = 12 \times 8 = 96 \, \text{cm}^3
$$
Contoh 4: Volume Limas Segi Empat
Sebuah limas segi empat memiliki luas alas 20 cm² dan tinggi 6 cm. Hitunglah volumenya!
Penyelesaian:
$$
V = \frac{1}{3} \times L_{\text{alas}} \times t = \frac{1}{3} \times 20 \times 6 = 40 \, \text{cm}^3
$$
Contoh 5: Volume Tabung
Sebuah tabung memiliki jari-jari 3 cm dan tinggi 10 cm. Hitunglah volumenya!
Penyelesaian:
$$
V = \pi r^2 \times t = 3.14 \times 3^2 \times 10 = 3.14 \times 9 \times 10 = 282.6 \, \text{cm}^3
$$
Contoh 6: Volume Kerucut
Sebuah kerucut memiliki jari-jari 4 cm dan tinggi 9 cm. Hitunglah volumenya!
Penyelesaian:
$$
V = \frac{1}{3} \times \pi r^2 \times t = \frac{1}{3} \times 3.14 \times 4^2 \times 9 = \frac{1}{3} \times 3.14 \times 16 \times 9 = 150.72 \, \text{cm}^3
$$
Contoh 7: Volume Bola
Sebuah bola memiliki jari-jari 7 cm. Hitunglah volumenya!
Penyelesaian:
$$
V = \frac{4}{3} \times \pi r^3 = \frac{4}{3} \times 3.14 \times 7^3 = \frac{4}{3} \times 3.14 \times 343 = 1436.02 \, \text{cm}^3
$$
Tips dan Trik Menghitung Volume Bangun Ruang
Menghitung volume bangun ruang bisa menjadi tantangan tersendiri, terutama jika ukuran atau bentuknya kompleks. Berikut ini beberapa tips dan trik yang bisa membantu dalam proses perhitungan:
-
Memahami Bentuk Alas
Setiap bangun ruang memiliki bentuk alas yang berbeda. Pastikan Anda mengetahui luas alas dari bangun ruang tersebut sebelum menghitung volumenya. Misalnya, untuk prisma segitiga, luas alasnya adalah luas segitiga, sedangkan untuk prisma persegi, luas alasnya adalah luas persegi. -
Gunakan Rumus yang Tepat
Pastikan Anda menggunakan rumus yang sesuai dengan jenis bangun ruang yang diberikan. Jangan menggabungkan rumus dari berbagai bangun ruang, karena hal ini bisa menyebabkan kesalahan dalam perhitungan. -
Perhatikan Satuan Pengukuran
Pastikan semua ukuran yang digunakan memiliki satuan yang sama. Misalnya, jika panjang sisi diberikan dalam centimeter, maka hasil akhir juga harus dalam sentimeter kubik. -
Latihan Teratur
Latihan teratur dengan berbagai jenis soal akan membantu Anda memahami konsep volume bangun ruang secara lebih baik. Coba kerjakan soal-soal dari buku teks atau situs web edukasi untuk meningkatkan kemampuan Anda. -
Gunakan Kalkulator
Jika perhitungan terlalu rumit, gunakan kalkulator untuk memastikan hasilnya akurat. Namun, jangan terlalu bergantung pada kalkulator; pastikan Anda memahami langkah-langkah perhitungan. -
Pahami Konsep Dasar Geometri
Pemahaman tentang konsep dasar geometri seperti luas, keliling, dan volume sangat penting. Jika Anda kurang memahami konsep dasar, sulit untuk menghitung volume bangun ruang dengan benar.
Manfaat Memahami Volume Bangun Ruang
Memahami volume bangun ruang tidak hanya bermanfaat dalam ujian matematika, tetapi juga memiliki manfaat dalam kehidupan nyata. Berikut ini beberapa manfaat yang bisa diperoleh dari pemahaman tentang volume bangun ruang:
-
Membantu dalam Perencanaan Konstruksi
Dalam bidang arsitektur dan konstruksi, volume bangun ruang digunakan untuk menghitung kapasitas ruangan, jumlah bahan bangunan yang diperlukan, atau pengaturan sistem ventilasi dan pendingin ruangan. -
Meningkatkan Kemampuan Logika dan Matematika
Menghitung volume bangun ruang melatih kemampuan logika dan analisis. Hal ini sangat bermanfaat dalam memecahkan masalah yang kompleks. -
Membantu dalam Pengambilan Keputusan
Dalam kehidupan sehari-hari, pemahaman tentang volume bisa membantu dalam pengambilan keputusan, seperti memilih wadah yang sesuai untuk menyimpan barang atau menghitung kapasitas air dalam tangki. -
Meningkatkan Keterampilan Teknis
Di bidang teknik, volume bangun ruang digunakan untuk merancang alat, mesin, atau sistem yang memerlukan pengukuran ketelitian. -
Membantu dalam Pendidikan
Bagi siswa, pemahaman tentang volume bangun ruang menjadi dasar untuk mempelajari materi matematika lanjutan seperti integral, persamaan diferensial, dan geometri analitis.
Kesimpulan
Volume bangun ruang adalah konsep matematika yang penting untuk dipahami. Dengan memahami berbagai jenis bangun ruang dan rumus volumenya, siswa dapat lebih mudah menyelesaikan soal-soal matematika yang berkaitan dengan bangun ruang. Contoh soal yang disertakan dalam artikel ini dapat membantu pembaca untuk melatih kemampuan mereka dalam menghitung volume. Selain itu, tips dan trik yang diberikan juga bisa membantu dalam proses belajar. Dengan latihan teratur dan pemahaman yang baik, siswa dapat meningkatkan kemampuan matematika mereka dan menghadapi ujian dengan lebih percaya diri. Pemahaman tentang volume bangun ruang juga memiliki manfaat dalam kehidupan nyata, baik dalam bidang teknik, konstruksi, maupun pengambilan keputusan sehari-hari. Dengan demikian, topik ini layak untuk dipelajari dan dikuasai oleh setiap siswa.





Komentar